|  | A rigid transformation (also called an isometry ) is a transformation of the plane that preserves length. Reflections, translations, rotations , and combinations of these three transformations are "rigid transformations". | 
While the pre-epitome and the image under a rigid transformation will be congruent,
they may non exist facing in the same direction. For a review of reflections, see the Refresher section Transformations: Reflections.
Now permit's expand that noesis of reflections in relation to geometry. A reflection over line m (annotation r m ) is a transformation in which each signal of the original figure (pre-image) has an image that is the same distance from the reflection line as the original point, but is on the opposite side of the line. A reflection is called a rigid transformation or isometry because the image is the same size and shape as the pre-image. 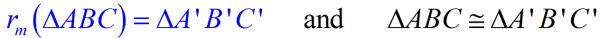
The reflection line, one thousand, is the perpendicular bisector o f the segments joining each point to its image.
Notice that these segments are parallel , since they are perpendicular to the same line. | 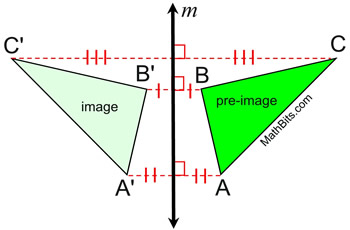 | In this reflection that maps ΔABC to ΔA'B'C', the distances from the pre-image points to the epitome points vary (are not necessarily equal), merely the segments representing these distances are parallel.
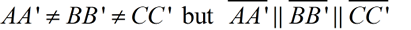 Orientation (lettering): The lettering of the points of the pre-image , in this diagram, is clockwise A-B-C, while the image is lettered counterclockwise A'-B'-C'. When lettering changes management, in this way, the transformation is referred to equally a non-directly or opposite isometry. | Properties preserved under a line reflection from the pre-image to the image.
1. distance (lengths of segments remain the same)
2. angle measures (remain the same)
3. parallelism (parallel lines remain parallel)
iv. collinearity (points remain on the same lines)
----------------------------------------------------------
The orientation (lettering around the outside of the figure), is not preserved . The club of the lettering in a reflection is reversed (from clockwise to counterclockwise or vice versa). | | When formally defining a reflection, there are ii situations (cases) that need to be considered for a precise definition. Is the betoken being reflected lying ON the line of reflection, or NOT ON the line of reflection?
 | A reflection is a rigid transformation (isometry) that maps every betoken P in the aeroplane to signal P', across a line of reflection, k, such that: |  For a review of translations, come across the Refresher section Transformations: Translations.
Now let's expand that knowledge of translations in relation to geometry. A translation (notation T a,b ) is a transformation which "slides" a effigy a stock-still distance in a given direction. In a translation, ALL of the points motion the same altitude in the same direction.
A translation is called a rigid transformation or isometry considering the image is the same size and shape as the pre-image. 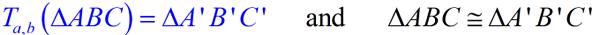 | | 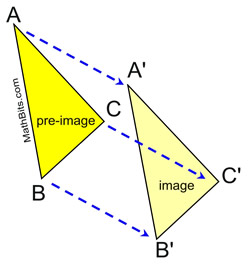 | In this translation that maps ΔABC to ΔA'B'C', the distances from the pre-image points to the image points are equal, and the segments representing these distances are parallel .
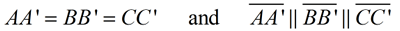
In addition, the corresponding segment sides of the pre-image and image are parallel. 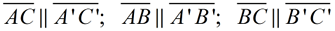
Orientation (lettering): The lettering of the points of the pre-epitome , in this diagram, is counterclockwise A-B-C, and the paradigm is also lettered counterclockwise A'-B'-C'. When lettering club remains the same, the transformation is referred to as a direct isometry. | Properties preserved under a translation from the pre-epitome to the image.
1. distance (lengths of segments remain the aforementioned)
2. angle measures (remain the aforementioned)
iii. parallelism (parallel lines remain parallel)
4. collinearity (points remain on the same lines)
v. orientation (lettering order remains the same)
| |  | A translation is a rigid transformation of the plane that moves every bespeak of a pre-paradigm a constant altitude in a specified direction. | There are several ways to indicate that a translation is to occur: | mapping:
Case:
(x, y) → (x + 8, y - vi)
Read: "the 10 and y coordinates are mapped to 10 + eight and y - half dozen respectively".
| notations:
Example: T 8,-6 or
T 8,-6 (10, y) = (x + 8, y - six)
The 8 tells you to "add viii" to all x-coordinates, while the -six tells yous to "decrease 6" from all of the y-coordinates.
| clarification:
Example:
"8 units to the right and vi units downwards." A exact or written description of the translation is given. | | Movement: Remember that adding a negative value (subtracting), indicates movement left and/or down , while adding a positive value indicates movement right and/or up . | | Using vectors to testify move of a translation: A vector is represented by a directed line segment, a segment with an pointer at 1 end indicating the direction of move. Unlike a ray, a directed line segment has a specific length. The Pythagorean Theorem can be used to find the length of a vector in the coordinate plane. Vectors used in translations are what are known as "complimentary vectors", which are a set of parallel directed line segments. A vector translation moving "8 units to the right and half-dozen units downwards" can be written as 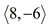 . You lot may also see . You lot may also see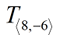 . . | | There is an "identity" translational transformation that maps all points onto themselves (no move of the pre-image), expressed every bit (x, y) → (x, y). (Y'all may meet the identity transformation denoted past the letter I.)  For a review of rotations, come across the Refresher section Transformations: Rotations.
Now let'south expand that knowledge of rotations in relation to geometry. A rotation of θ degrees (annotation RC,θ ) is a transformation which "turns" a figure about a fixed point, C, chosen the center of rotation . When working in the coordinate plane, the center of rotation should exist stated, and not causeless to be at the origin. Rays drawn from the eye of rotation to a point and its paradigm class an bending called the angle of rotation . A rotation is called a rigid transformation or isometry because the epitome is the same size and shape as the pre-image. 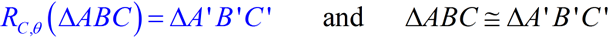
An object and its rotation are the same shape and size, but the figures may be positioned differently. During a rotation, every bespeak is moved the verbal same degree arc along the circumvolve
divers by the eye of the rotation and the angle of rotation.
(The dashed arcs in the diagram beneath represent the circles, with center P, through each of the triangle's vertices.
Notation that PC=PC', for instance, since they are the radii of the same circumvolve.) A positive angle of rotation turns a figure counterclockwise (CCW),
and a negative bending of rotation turns the effigy clockwise, (CW). | 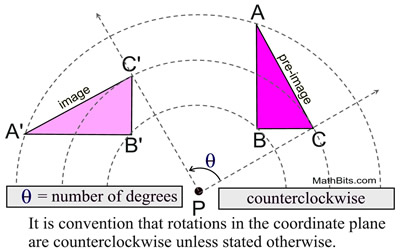 | In this rotation that maps ΔABC to ΔA'B'C', the distances from the pre-image points to the paradigm points vary (as they are the radii of the circles). Dissimilar reflections and translations, the segments connecting pre-prototype and image points are NOT parallel.
Orientation (lettering): The lettering of the points of the pre-image , in this diagram, is counterclockwise A-B-C, and the image is also lettered counterclockwise A'-B'-C'. | Properties preserved nether a rotation from the pre-paradigm to the image.
1. distance (lengths of segments remain the same)
ii. angle measures (remain the same)
3. parallelism (parallel lines remain parallel)
4. collinearity (points remain on the aforementioned lines)
5. orientation (lettering order remains the same) | Common Graph Rotations:
(center at the origin, O)
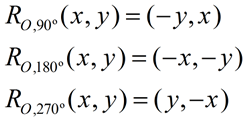
Encounter rotation "examples" on the page
Transformations: Rotations. | There are 2 possible directions to travel when rotating. Look at point P in the diagram at the right. The positive x-axis is considered the "starting" location of 0º. You lot tin have an bending of rotation of positive 135º counterclockwise to bespeak P, or a negative angle of 225º clockwise to point P.
Detect that together, the angles (135º and 225º) class a consummate circle (360º). It is fifty-fifty possible to have one complete revolution (360º) PLUS and additional 135º to get to P (an bending of rotation of 495º). | 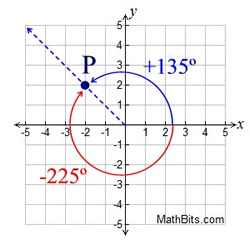 | | When working in the coordinate aeroplane, it is important to take a visual understanding of how the quadrants are divided through rotational angles. The most mutual angles seen on the grid are multiples of 15º. The "favorite" angles are usually 30º, 45º, 60º, 90º, 180º, and 270º. | 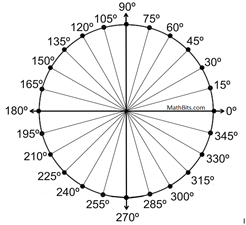 | | There is an "identity" rotational transformation of 0º that maps all points onto themselves (no move of the pre-image), written RC,0 (P) = P. (You may likewise see the identity transformation denoted by the alphabetic character I.)
| 
Notation: The re-posting of materials (in function or whole) from this site to the Internet is copyright violation
and is not considered "fair use" for educators. Delight read the "Terms of Use". | |





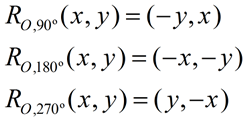



0 Response to "All Transformations That Maintain Both Their Shape And Size Are Known As What?"
Post a Comment